KINEMATIK GERAK TRANSLASI DAN ROTASI
Kinematika Gerak dan RotasiHanya dengan menggunakan intuisi kita, kita dapat mulai melihat bagaimana besaran rotasi seperti θ , ω , dan α berhubungan satu sama lain. Misalnya, jika sebuah roda sepeda motor mempunyai percepatan sudut yang besar dalam waktu yang cukup lama, maka roda tersebut akan berputar dengan cepat dan berputar melalui banyak putaran. Dalam istilah yang lebih teknis, jika percepatan sudut roda α besar untuk jangka waktu yang lama t , maka kecepatan sudut akhir ω dan sudut rotasi θ juga besar. Gerak rotasi roda dianalogikan dengan percepatan translasi sepeda motor yang besar menghasilkan kecepatan akhir yang besar, dan jarak yang ditempuh juga akan besar.
Kinematika adalah deskripsi gerak. Kinematika gerak rotasi menggambarkan hubungan antara sudut rotasi, kecepatan sudut, percepatan sudut, dan waktu. Mari kita mulai dengan mencari persamaan yang berhubungan dengan ω , α , dan t . Untuk menentukan persamaan ini, kita mengingat persamaan kinematik yang sudah dikenal untuk gerak translasi atau garis lurus:
Perhatikan bahwa dalam gerak rotasi a = at , dan mulai sekarang kita akan menggunakan simbol a untuk percepatan tangensial atau linier. Seperti dalam kinematika linier, kita asumsikan a konstan, artinya percepatan sudut α juga konstan, karena a = rα . Sekarang, mari kita substitusikan v = rω dan a = rα ke dalam persamaan linear di atas:
rω = rω 0 + tikus.
Jari-jari r dihilangkan dalam persamaan, menghasilkan
ω = ω 0 + pada. (konstanta a )
di mana ω 0 adalah kecepatan sudut awal. Persamaan terakhir ini adalah hubungan kinematis antara ω , α , dan t —yaitu, persamaan ini menggambarkan hubungan keduanya tanpa mengacu pada gaya atau massa yang dapat mempengaruhi rotasi. Bentuknya juga sama persis dengan bentuk translasinya.
MEMBUAT KONEKSI
Kinematika untuk gerak rotasi sepenuhnya analog dengan kinematika translasi, yang pertama kali disajikan dalam kinematika satuan dimensi . Kinematika berkaitan dengan deskripsi gerak tanpa memperhatikan gaya atau massa. Kita akan menemukan bahwa besaran kinematik translasi, seperti perpindahan, kecepatan, dan percepatan memiliki analogi langsung dengan gerak rotasi.Dimulai dengan empat persamaan kinematik yang kami kembangkan dalam Kinematika satuan Dimensi,kita dapat memperoleh empat persamaan kinematik rotasi berikut (disajikan bersama dengan persamaan translasinya):
Tabel 1. Persamaan Kinematik RotasiRotasi Terjemahan ω = ω 0 + αt v = v o + pada (konstanta α , a ) (konstanta α , a ) ω 2 = ω 0 2 + 2 α θ v 2 = v o 2 + 2ax (konstanta α , a )
Dimulai dengan empat persamaan kinematik yang kami kembangkan dalam Kinematika satuan Dimensi,kita dapat memperoleh empat persamaan kinematik rotasi berikut (disajikan bersama dengan persamaan translasinya):
| Rotasi | Terjemahan | |
|---|---|---|
| ω = ω 0 + αt | v = v o + pada | (konstanta α , a ) |
| (konstanta α , a ) | ||
| ω 2 = ω 0 2 + 2 α θ | v 2 = v o 2 + 2ax | (konstanta α , a ) |
Dalam persamaan ini, subskrip 0 menunjukkan nilai awal ( θ 0 , x 0 , dan t 0 adalah nilai awal), dan kecepatan sudut rata-rata dan kecepatan rata-rata didefinisikan sebagai berikut:
.
Persamaan yang diberikan di atas pada Tabel 1 dapat digunakan untuk menyelesaikan masalah kinematika rotasi atau translasi dimana a dan α konstan.
LINGKUP KINEMATIKA
Pada kinematika dibahas tentang semua jenis gerak, baik gerak satu dimensi atau gerak dua dimensi. Gerak satu dimensi adalah gerak benda sepanjang garis lurus yang terjadi pada satu arah atau sumbu.
Contoh gerak satu dimensi adalah gerak lurus beraturan (straight line motion with constant velocity) , gerak lurus berubah beraturan (straight line motion with constant acceleration), gerak vertikal ke atas (vertical upward motion), dan gerak jatuh bebas (vertical motion under gravity)
Selain itu, terdapat gerak dua dimensi. Gerak dua dimensi adalah gerak benda yang terjadi pada dua arah atau sumbu. Contoh gerak dua dimensi adalah gerak parabola (projectile motion), gerak melingkar beraturan (uniform circular motion), dan gerak melingkar berubah beraturan (non-uniform circular motion).
Contoh gerak satu dimensi adalah gerak lurus beraturan (straight line motion with constant velocity) , gerak lurus berubah beraturan (straight line motion with constant acceleration), gerak vertikal ke atas (vertical upward motion), dan gerak jatuh bebas (vertical motion under gravity)
Suatu benda dapat mengalami gerak translasi atau gerak rotasi. Gerak translasi adalah gerak benda yang arahnya lurus ataupun melengkung. Pada gerak translasi menggunakan konsep hukum Newton II. Sedangkan gerak rotasi adalah gerak yang mengalami perputaran terhadap poros tertentu. Gerak rotasi ini disebabkan oleh adanya torsi yaitu kecenderungan sebuah gaya untuk memutar suatu benda tegar terhadap titik poros tertentu.
Gerak pada rotasi mengalami suatu torsi. Torsi adalah ukuran kecenderungan sebuah gaya untuk memutar suatu benda tergar terhadap titik poros tertentu. Rumusan Torsi/momen gaya adalah sebagai berikut:

Lengan Momen
Lengan momen (l) adalah sebutan untuk jarak titik poros rotasi sampai ke gaya yang saling tegak lurus.
Torsi merupakan suatu besaran vektor. Sehingga ia mempunyai arah. Torsi bernilai positif (+) apabila arahnya berlawanan jarum jam. Sedangkan torsi bernilai negatif (-) apabila arahnya searah dengan jarum jam.
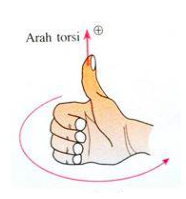
Lengan momen (l) adalah sebutan untuk jarak titik poros rotasi sampai ke gaya yang saling tegak lurus.
Torsi merupakan suatu besaran vektor. Sehingga ia mempunyai arah. Torsi bernilai positif (+) apabila arahnya berlawanan jarum jam. Sedangkan torsi bernilai negatif (-) apabila arahnya searah dengan jarum jam.

Momen Inersia
Dalam dinamika rotasi juga dikenal istilah penting yaitu momen inersia. Momen inersia adalah besaran yang menyatakan ukuran kelembaman benda yang mengalami gerak rotasi adalah momen inersia (analog dengan massa pada gerak translasi). Rumusan momen inersia adalah sebagai berikut:

Di mana
I = momen inersia (kg m2)
m = massa benda (kg)
r = jari-jari benda (m)
Tiap benda memiliki nilai momen inersianya masing-masing, berikut adalah nilai dari momen inersia yang sering dipakai dalam masalah kesetimbangan benda tegar:
Dalam dinamika partikel, kita mengetahui bahwa gaya F menyebabkan suatu benda bergerak translasi dengan percepatan linear a. Dan suatu torsi τ menyebabkan suatu benda berotasi terhadap suatu poros tertentu. Oleh karena torsi τ analog dengan gaya F dan percepatan sudut α analog dengan percepatan linear a. sehingga dapat dihasilkan hukum II Newton untuk suatu rotasi yaitu sebagai berikut:

Di mana:
I = momen inersia (kg m2)
α = percepatan sudut (rad/s2)
τ = torsi (N .m)
r = jarak titik ke poros (m)
Cara menghitung energi kinetik rotasi dari suatu massa adalah sebagai berikut:
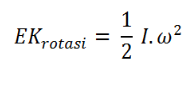
Persamaan di atas menyatakan energi kinetik dari suatu benda tegar yang momen inersianya I dan berputar dengan kecepatan sudut ω. Apabila suatu benda dalam keadaan menggelinding. Dalam dinamika rotasi, gerak menggelinding adalah suatu benda tegar bergerak translasi dalam suatu ruang sambil berotasi tanpa slip. Nilai Energi Kinetik pada saat benda menggelinding adalah sebagai berikut:

Contoh 1: Benda menggelinding dan SOLUSI SUPER
Pada gambar di bawah menunjukkan sebuah benda menggelinding dari atas menuju alas bidang. Nilai percepatan benda tersebut dapat ditentukan menggunakan rumus hukum kekekalan energi. Namun kita akan menggunakan rumus SOLUSI SUPER untuk menentukan nilai percepatan dan kecepatan dari benda tersebut yaitu:
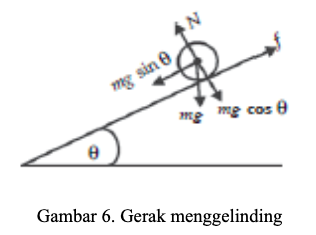
Nilai percepatan (a) pada saat benda menggelinding dari atas:
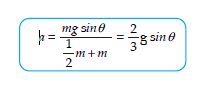
Nilai kecepatan (v) pada saat benda menggelinding di atas:

Dari persamaan di atas, terdapat konstanta k. nilai k dapat dirubah dengan momen inersia yang ditunjukkan pada gambar 5. Contohnya sebagai berikut:

Contoh 2: Sebuah rotasi silinder yang dilekatkan pada tali
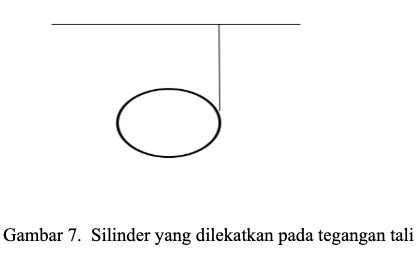
Nilai percepatan silinder ( a) nya dapat ditentukan dengan:
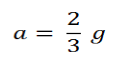
Dan nilai tegangan tali (T) nya dapat ditentukan dengan:
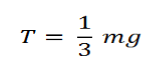
Contoh 3: Sebuah sistem katrol dengan massa dan bola yang saling menurun
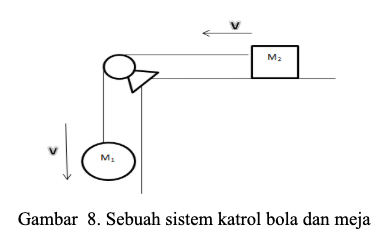
Nilai percepatan kedua benda tersebut dapat ditentukan dengan
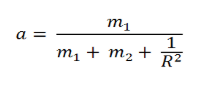
Contoh 4: Gerak menggelinding benda pejal mendaki suatu bidang miring

Nilai ketinggian suatu bidang miring (h) dapat ditentukan menggunakan persamaan:

Nilai jaraknya (s) dapat ditentukan dengan cara:
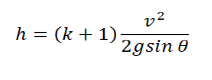
Dinamika rotasi merupakan ilmu yang mempelajari pergerakan benda berputar pada porosnya. Gerak benda tersebut mengelilingi sumbu putar (rotasi) yang dipengaruhi oleh gaya, massa, momen inersia, dan lainnya. Namun, benda dalam dinamika rotasi dianggap memiliki ukuran dan bentuk yang tetap.
Dinamika rotasi dapat terjadi pada benda yang bergerak di lintasan yang lurus. Jika benda bergerak lurus dikatakan translasi, sedangkan benda yang bergerak di lintasan melingkar disebut dengan rotasi. Besaran yang memengaruhi dinamika rotasi di antaranya sebagai berikut.
Dalam dinamika rotasi juga dikenal istilah penting yaitu momen inersia. Momen inersia adalah besaran yang menyatakan ukuran kelembaman benda yang mengalami gerak rotasi adalah momen inersia (analog dengan massa pada gerak translasi). Rumusan momen inersia adalah sebagai berikut:

Di mana
I = momen inersia (kg m2)
m = massa benda (kg)
r = jari-jari benda (m)
Tiap benda memiliki nilai momen inersianya masing-masing, berikut adalah nilai dari momen inersia yang sering dipakai dalam masalah kesetimbangan benda tegar:
Dalam dinamika partikel, kita mengetahui bahwa gaya F menyebabkan suatu benda bergerak translasi dengan percepatan linear a. Dan suatu torsi τ menyebabkan suatu benda berotasi terhadap suatu poros tertentu. Oleh karena torsi τ analog dengan gaya F dan percepatan sudut α analog dengan percepatan linear a. sehingga dapat dihasilkan hukum II Newton untuk suatu rotasi yaitu sebagai berikut:

Di mana:
I = momen inersia (kg m2)
α = percepatan sudut (rad/s2)
τ = torsi (N .m)
r = jarak titik ke poros (m)
Cara menghitung energi kinetik rotasi dari suatu massa adalah sebagai berikut:
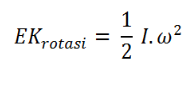
Persamaan di atas menyatakan energi kinetik dari suatu benda tegar yang momen inersianya I dan berputar dengan kecepatan sudut ω. Apabila suatu benda dalam keadaan menggelinding. Dalam dinamika rotasi, gerak menggelinding adalah suatu benda tegar bergerak translasi dalam suatu ruang sambil berotasi tanpa slip. Nilai Energi Kinetik pada saat benda menggelinding adalah sebagai berikut:

Contoh 1: Benda menggelinding dan SOLUSI SUPER
Pada gambar di bawah menunjukkan sebuah benda menggelinding dari atas menuju alas bidang. Nilai percepatan benda tersebut dapat ditentukan menggunakan rumus hukum kekekalan energi. Namun kita akan menggunakan rumus SOLUSI SUPER untuk menentukan nilai percepatan dan kecepatan dari benda tersebut yaitu:

Nilai percepatan (a) pada saat benda menggelinding dari atas:
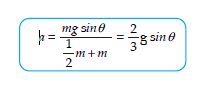
Nilai kecepatan (v) pada saat benda menggelinding di atas:

Dari persamaan di atas, terdapat konstanta k. nilai k dapat dirubah dengan momen inersia yang ditunjukkan pada gambar 5. Contohnya sebagai berikut:

Contoh 2: Sebuah rotasi silinder yang dilekatkan pada tali

Nilai percepatan silinder ( a) nya dapat ditentukan dengan:
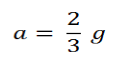
Dan nilai tegangan tali (T) nya dapat ditentukan dengan:
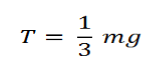
Contoh 3: Sebuah sistem katrol dengan massa dan bola yang saling menurun

Nilai percepatan kedua benda tersebut dapat ditentukan dengan
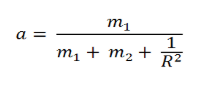
Contoh 4: Gerak menggelinding benda pejal mendaki suatu bidang miring

Nilai ketinggian suatu bidang miring (h) dapat ditentukan menggunakan persamaan:

Nilai jaraknya (s) dapat ditentukan dengan cara:
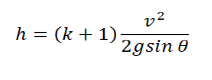
Dinamika rotasi merupakan ilmu yang mempelajari pergerakan benda berputar pada porosnya. Gerak benda tersebut mengelilingi sumbu putar (rotasi) yang dipengaruhi oleh gaya, massa, momen inersia, dan lainnya. Namun, benda dalam dinamika rotasi dianggap memiliki ukuran dan bentuk yang tetap.
Dinamika rotasi dapat terjadi pada benda yang bergerak di lintasan yang lurus. Jika benda bergerak lurus dikatakan translasi, sedangkan benda yang bergerak di lintasan melingkar disebut dengan rotasi. Besaran yang memengaruhi dinamika rotasi di antaranya sebagai berikut.
1. Torsi (Momen Gaya)
Torsi merupakan besaran gaya yang bekerja, sehingga benda bergerak melingkar. Benda bergerak di porosnya, misalnya saja putaran jarum jam.
2. Gerak Rotasi
Energi dan gerak rotasi memengaruhi dinamika rotasi. Energi kinetik merupakan benda yang bergerak menggelinding. Ketika dijumlahkan, nilai itu dinamakan dengan energi kinetik benda yang menggelinding. Selain energi, benda bergerak di porosnya juga mempunyai gaya.
3. Momentum Sudut
Momentum sudut merupakan ukuran kesukaran benda untuk mengubah arah gerak benda ketika berputar atau bergerak melingkar.
Rumus Dinamika Rotasi
Dinamika rotasi dipengaruhi oleh torsi (momen inersia), percepatan, kecepatan, massa, dan gaya. Rumus dinamika rotasi memakai konsep Hukum II Newton.
Rumus dinamika rotasi Hukum II Newton sebagai berikut.
ΣF = m.a
Rumus dinamika rotasi yang dipengaruhi torsi sebagai berikut.
Στ = Ι.α
Keterangan:
- ΣF : resultan gaya.
- (N) m : massa/ukuran kelembaman (kg).
- a : percepatan (m/s2).
- Στ : momen torsi (Nm).
- I : momen inersia (kgm2).
- α : percepatan sudut (rad/s).
Contoh Soal
1.Silinder pejal dengan jari-jari 5 cm bermassa 0,25 kg bertranslasi dengan kelajuan linear 4 m/s. Tentukan energi kinetik silinder jika selain bertranslasi silinder juga berotasi!
Pembahasan
Data dari soal:
m = 0,25 kg
r = 5 cm = 0,05 m
v = 4 m/s
Ek =…..
Energi kinetik total dari silinder pejal:
2.Sebuah balok yang massanya 6 kg meluncur ke bawah pada sebuah papan licin yang dimiringkan 30ᵒ dari lantai. Jika jarak lantai dengan balok 10 m dan besarnya percepatan gravitasi di tempat itu adalah 10 ms-2, maka tentukan percepatan dan waktu yang diperlukan balok untuk sampai di lantai.JawabDiketahui:m = 6 kgs = 10 mθ = 30ᵒ
g = 10 m/s
Ditanyakan: Percepatan dan waktu.
Langkah pertama untuk menyelesaikan soal yang berhubungan dengan dinamika gerak adalah menggambarkan skema ilustrasi soal beserta diagram gaya yang bekerja pada sistem seperti yang ditunjukkan pada gambar di bawah ini.
 Karena kondisi bidang miring adalah licin, maka tidak ada gaya gesek sehingga kita tidak perlu menguraikan resultan gaya pada sumbu-Y atau sumbu vertikal. Menurut Hukum II Newton, resultan gaya yang bekerja pada benda dalam arah sumbu-X adalah sebagai berikut.ΣFX = maw sin θ = mamg sin θ = maa = g sin θ …………… Pers. (1)
Karena kondisi bidang miring adalah licin, maka tidak ada gaya gesek sehingga kita tidak perlu menguraikan resultan gaya pada sumbu-Y atau sumbu vertikal. Menurut Hukum II Newton, resultan gaya yang bekerja pada benda dalam arah sumbu-X adalah sebagai berikut.ΣFX = maw sin θ = mamg sin θ = maa = g sin θ …………… Pers. (1)
■ Menentukan percepatanUntuk menentukan besar percepatan balok, subtitusikan nilai-nilai yang diketahui dalam soal ke persamaan (1) sebagai berikut.a = g sin θa = (10)(sin 30ᵒ)a = (10)(0,5)a = 5 m/s2jadi, balok tersebut meluncur ke bawah dengan percepatan sebesar 5 m/s2.
■ Menentukan waktu untuk sampai di lantaiUntuk menentukan waktu yang diperlukan balok untuk mencapai lantai, kita gunakan rumus jarak pada gerak lurus berubah beraturan atau GLBB. (Kenapa GLBB bukan GLB?).s = v0t + ½ at2karena tidak ada keterangan mengenai kecepatan awal, maka v0 = 0 sehinggas = ½ at2t2 = 2s/at = √(2s/a) …………… Pers. (2)Subtitusikan besar percepatan dan nilai yang diketahui dalam soal ke persamaan (2)t = √[(2)(10)/5]t = √(20/5)t = √4t = 2 m/s2Dengan demikian, waktu yang diperlukan balok untuk sampai ke lantai adalah 2 detik.
referensi:https://www.fisikabc.com/2018/06/contoh-soal-dinamika-partikel-gerak-translasi-2.htmlhttps://www.gramedia.com/literasi/contoh-soal-dinamika-rotasi/https://www.texasgateway.org/resource/102-kinematics-rotational-motionhttps://www.quipper.com/id/blog/mapel/fisika/dinamika-rotasi-fisika-kelas-11/
θ = 30ᵒ
g = 10 m/s
Ditanyakan: Percepatan dan waktu.
Langkah pertama untuk menyelesaikan soal yang berhubungan dengan dinamika gerak adalah menggambarkan skema ilustrasi soal beserta diagram gaya yang bekerja pada sistem seperti yang ditunjukkan pada gambar di bawah ini.


Komentar
Posting Komentar